Fahren Sie jeden Morgen mit dem Auto oder mit dem Bus zur Arbeit? Welche Verkehrslage erwartet Sie? Hätten Sie lieber den Bus oder das eigene Auto nehmen sollen? All diese Fragen werden mit Hilfe der App Go!Track beantwortet. Go!Track ist eine App für Android-User, die in der Stadt Aracuja im östlichen Teil Brasiliens genutzt wird. Die App bietet nützliche Hilfestellungen für den täglichen Verkehr an. Sie ist in der Lage, Routen zu empfehlen, Vorhersagen der Ankunfts- und Abfahrtszeit mit dem Bus zu treffen und Staus oder sogar das Reisewetter vorherzusagen. Nur durch die Eingaben der Nutzer können diese Vorhersagen getroffen werden. Die gesammelten Daten über den Bus- und Autoverkehr in Aracuja werden in dem Datensatz „GPS-Trajectories“ zur Verfügung gestellt.
Der Datensatz besteht aus 163 Routen von 28 verschiedenen mobilen Geräten unterschiedlicher Benutzer, die in den Jahren von 2014 bis Anfang 2016 gesammelt wurden. Durch die Angaben der Benutzer der Go!Track App kann in dem Datensatz zwischen den Verkehrsmitteln PKW und Bus unterschieden und überprüft werden, welches Fortbewegungsmittel voraussichtlich das schnellere sein wird.
Welche Daten liegen vor?
Der frei verfügbare Datensatz umfasst zwei Tabellen. In der ersten Tabelle „go_track_tracks“ wurden alle Informationen über die gesammelten Routen gespeichert, während in der zweiten Tabelle „go_track_trackpoints“ die geografischen Punkte notiert wurden. Dieser Blogartikel fokussiert sich auf „go_track_tracks“. Der Datensatz enthält 163 Beobachtungen mit 10 Variablen.
Die Variablen der „go_track_tracks“-Tabelle beinhalten folgende Informationen:
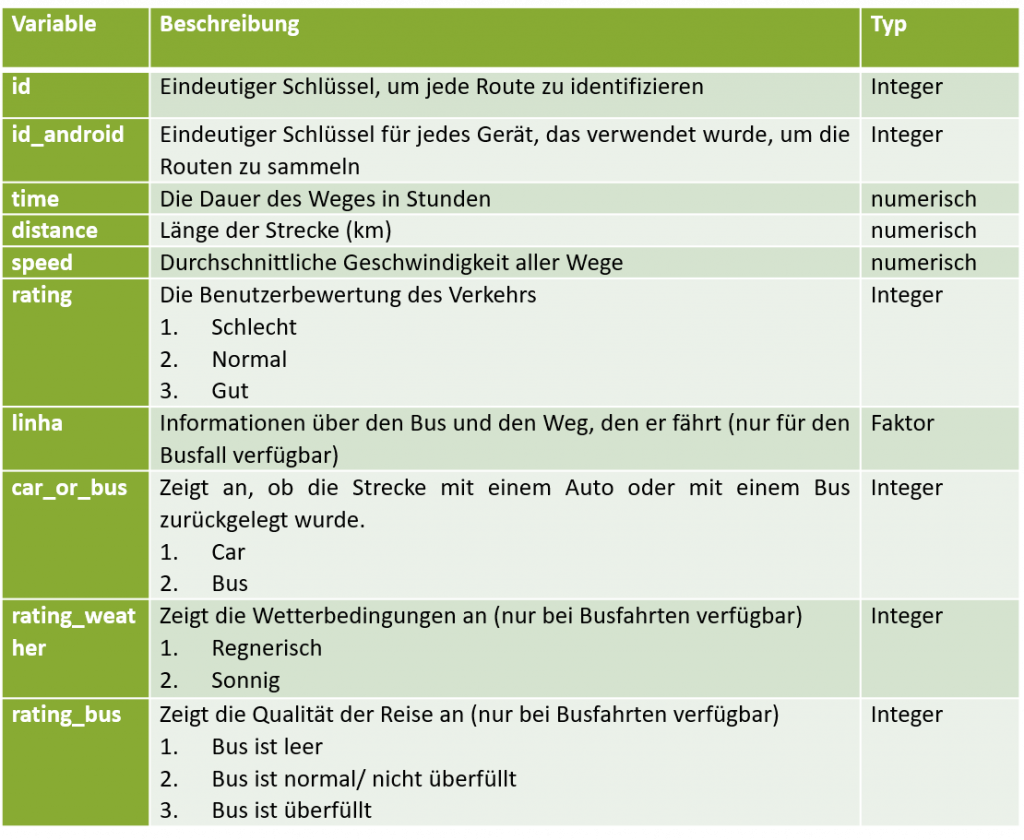
Man sieht, dass der Datensatz sechs Variablen vom Typ Integer, drei numerische und eine Faktorvariable enthält. Am inhaltlich interessantesten erscheinen die drei numerischen Variablen speed, time und distance. Diese eignen sich ebenfalls sehr gut für multivariate Verfahren, da sie alle ein metrisches Skalenniveau haben. Außerdem ist die Variable car_or_bus interessant, um die Frage zu beantworten, welches Verkehrsmittel seine Passagiere in kürzerer Zeit von A nach B bringt. Anzeichen für Zusammenhänge zwischen speed, time und distance kann uns eine Korrelationsmatrix liefern:
go_track_tracks_analyse < - go_track_tracks %>% select(speed, time, distance)
cor(go_track_tracks_analyse)
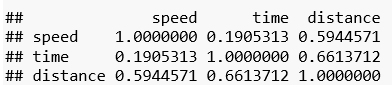
Die Korrelationsmatrix zeigt die erwartbaren Zusammenhänge zwischen Geschwindigkeit (speed) und Distanz (distance) sowie zwischen Dauer (time) und Distanz. Der Zusammenhang zwischen Dauer und Geschwindigkeit scheint hingegen nicht sehr groß zu sein.
Einsatzgebiet: Multivariate Statistik
GPS-Trajectories eignet sich für den Bereich der multivariaten Statistik, da metrische Werte mehrerer Variablen vorliegen. Mit Hilfe der multivariaten Statistik können Zusammenhänge und Abhängigkeiten erkannt werden. Unterschieden wird zwischen strukturentdeckenden und strukturprüfenden Verfahren. Wir zeigen im Folgenden, wie der Datensatz für eine Cluster- und Regressionsanalyse verwendet werden kann.
Anwendung eines strukturentdeckenden Verfahrens – Welche Muster ergeben sich?
Was bietet sich an, um einen noch besseren Überblick über die Fälle zu erhalten ohne vorher vorzugeben, wie man diese zu klassifizieren hat? Eine Clusteranalyse. Im Folgenden wurden drei Cluster nach den Variablen speed, time, distance und car_or_bus mit der K-Means-Methode erstellt und mittels ggplot grafisch dargestellt.
# k-means algorithm with 3 centers, run 20 times
Cluster < - as.factor(kmeans(go_track_tracks_analyse, centers = 3, nstart = 20)$cluster)
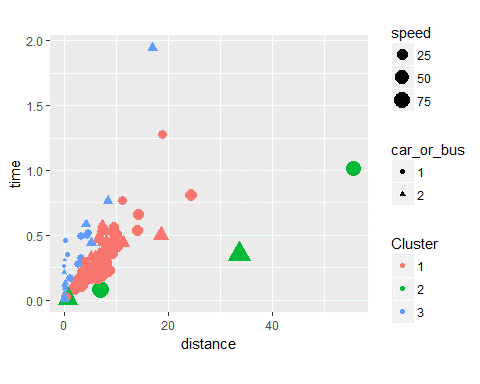
Grafisch lässt sich erkennen, dass Cluster 2 eine kleine Anzahl verhältnismäßig schnellerer Fahrten enthält. Dies sieht man daran, dass sie in einem Bereich liegen, in dem das Weg/Zeit-Verhältnis hoch ist und auch die Durchschnittsgeschwindigkeit einen hohen Wert annimmt. Bei Cluster 3 ist es genau umgekehrt, hier ist die Durchschnitts-geschwindigkeit eher gering und die Fälle liegen in einem Bereich, in dem das Weg/Zeit-Verhältnis ebenfalls gering ist. Das Cluster 1 beinhaltet die meisten Fahrten und liegt im Mittelfeld zwischen den extremeren Clustern. Sie scheinen ungefähr auf einer Linie zu liegen.
Anwendung eines strukturüberprüfenden Verfahrens – Wie lange dauert meine Fahrt?
Wie genau ein linearer Zusammenhang aussehen könnte, lässt sich mittels linearer Regression bestimmen. Was ist das Ziel dieser Analyse? Ob es einen Zusammenhang zwischen der Dauer und dem Verkehrsmittel gibt, kann man grafisch noch nicht feststellen. Hier kann eine Regression hilfreich sein. Auch die Einflüsse von Distanz und Geschwindigkeit auf die Dauer bleiben eher Vermutungen auf Basis grafischer Schätzungen. Dabei könnte die Regression eine verlässlichere Antwort geben. Inhaltlich bleiben also die Fragen danach,
- ob nur die Streckendistanz entscheidend ist;
- ob die Durchschnittsgeschwindigkeit einen signifikanten Einfluss hat;
- welchen Einfluss der Verkehr auf der Strecke auf die Dauer der Fahrt hat und
- ob es generell mit dem Auto oder dem Bus schneller geht.
Man möchte demnach herausfinden, worauf es zurückzuführen ist, dass einige Fahrten länger und andere kürzer dauern. Die logische Schlussfolgerung wäre: Längere Strecken ziehen auch länger dauernde Fahrten nach sich. Dies gilt es zu überprüfen. Außerdem stellt sich die Frage, ob die Distanz der einzige Faktor ist? Spielt nicht auch die Durchschnittsgeschwindigkeit eine Rolle?
Um die Bewertung des Verkehrs noch in das Modell mit aufzunehmen, muss die Variable rating erst in eine Faktorvariable umgewandelt werden (hier mit dplyr). Eine Aufnahme dieser kategorialen Variable führt dazu, dass das Level 1 (Benutzerbewertung über den Verkehr: Schlecht) als Referenzkategorie genutzt wird.
go_track_tracks < - go_track_tracks %>% mutate(rating = as.factor(rating))
Regressieren wir nun die Zeit (time) auf die Variablen distance, speed und rating erhalten wir den folgenden Output:
fit < - lm(data = go_track_tracks, time ~ distance + speed + rating) summary(fit)
##
## Call:
## lm(formula = time ~ distance + speed + rating, data = go_track_tracks
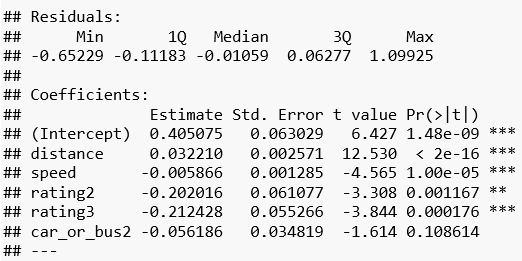
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2016 on 158 degrees of freedom
## Multiple R-squared: 0.5372, Adjusted R-squared: 0.5255
## F-statistic: 45.85 on 4 and 158 DF, p-value: < 2.2e-16
Das Ergebnis bestätigt, die Distanz und Geschwindigkeit haben einen hochsignifikanten Einfluss auf die Variable time. Erhöht sich die Länge der Strecke um einen Kilometer, so steigt die geschätzte Fahrdauer unter Konstanthaltung aller anderen unabhängigen Variablen um knapp 0,03 Stunden, also fast 2 Minuten. Im Gegensatz dazu verringert sich die Dauer erwartungsgemäß bei einer höheren Durchschnittsgeschwindigkeit c.p.
Was geschieht zur Rush Hour?
Man sieht sowohl in der Regressionstabelle als auch in der nachfolgenden Grafik recht deutlich, dass eine schlechtere Verkehrssituation die Fahrzeit verlängert. Je besser der Verkehr bewertet ist, desto niedriger war die Fahrzeit time.
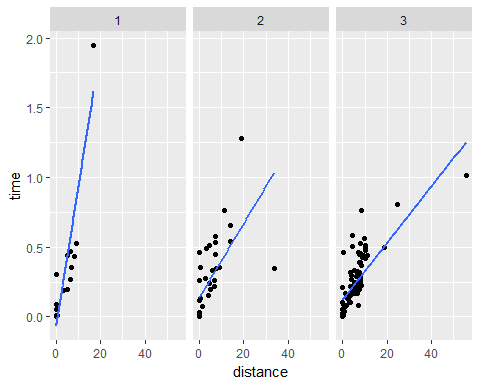
In der Grafik ist dies erkennbar daran, dass z.B. bei einer Strecke von 10 km die Fahrt bei schlechtem Verkehr (rating = 1) eine Stunde und bei gut bewertetem Verkehr (rating = 3) nur knapp 0,3 Stunden, also ca. 20 Minuten dauert.
Auto oder Bus?
So weit, so gut, aber auch nicht wirklich verwunderlich und aufschlussreich. Besonders interessant ist doch, ob es einen Unterschied macht, ob man das Auto oder den Bus nimmt. Dafür nehmen wir nun die Variable car_or_bus in unser Modell auf. Dabei dient die Kategorie Car als Referenzkategorie.
fit_car_or_bus < - lm(data = go_track_tracks, time ~ distance + speed + rating + car_or_bus) summary(fit_car_or_bus)
##
## Call:
## lm(formula = time ~ distance + speed + rating + car_or_bus, data = go_track_tracks)
##
## Residuals:
## Min 1Q Median 3Q Max ## -0.65229 -0.11183 -0.01059 0.06277 1.09925
##
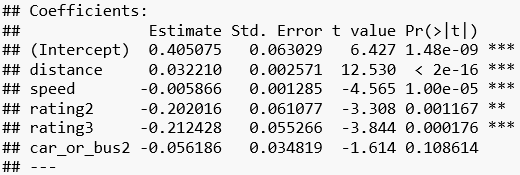
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2006 on 157 degrees of freedom
## Multiple R-squared: 0.5448, Adjusted R-squared: 0.5303
## F-statistic: 37.57 on 5 and 157 DF, p-value: < 2.2e-16
Die Regressionstabelle zeigt ein erstaunliches Resultat. Der Effekt von car_or_bus besagt zwar, dass es mit dem Bus länger dauert, jedoch liegt der p-Wert dieses Effekts über einer Irrtumswahrscheinlichkeit von 5% und der Effekt ist damit nicht signifikant.
Zusamenfassung aller Modelle
Hier kann man noch einmal gut verfolgen, wie sich die Effekte und auch die Modellgüte inklusive Varianzaufklärung bei Hinzunahme von Variablen in das Regressionsmodell verändern.
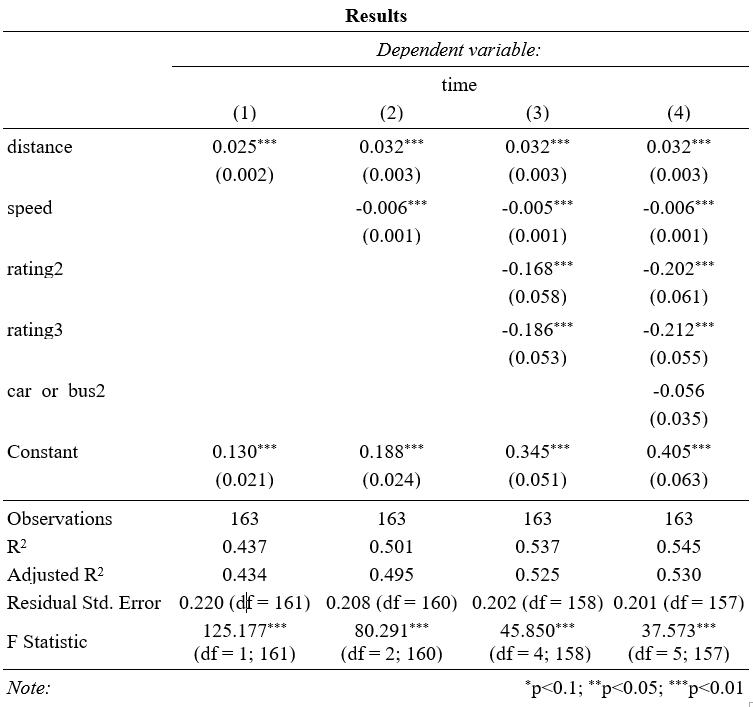
Das adjustierte R², welches um die Variablenanzahl im Modell korrigiert ist, erhöht sich von 43,4 % erklärter Varianz auf 53 %. Eine Hinzunahme der Geschwindigkeit erzeugt eine um fast 7 % erhöhte Erklärungskraft, während die Variablen Rating und Car_or_Bus nur zu einer geringfügigen Verbesserung der Modellgüte beitragen.
Ausblick
Gibt der Datensatz noch mehr her? Definitiv!
Denkbar wäre unter anderem, dass eine Analyse von Interaktionseffekten spannende Ergebnisse über die Effektzusammenhänge liefert. Des Weiteren lassen sich die Ergebnisse der Regressionsanalyse verwenden, um für neue Daten die Werte der abhängigen Variable zu prognostizieren. Dabei könnten die Variablen „rating_weather“ oder „rating_bus“ und „linha“ im Falle einer Busfahrt das Modell und seine Vorhersagegenauigkeit verbessern. Diese wiederum sind evaluierbar mit den Informationskriterien AIC und BIC. Und vielleicht fallen Ihnen ja noch weitere interessante Fragestellungen ein.
Also warum noch warten? Viel Spaß bei der Analyse der „GPS Trajectories“!
Dieser Beitrag ist Teil einer Open Data Blogserie, in der wir öffentlich verfügbare Datensätze vorstellen.